0x00 图

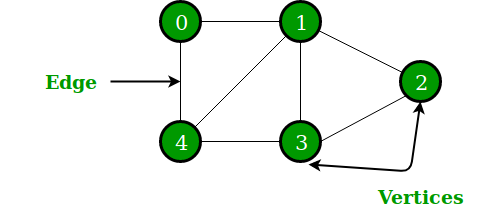
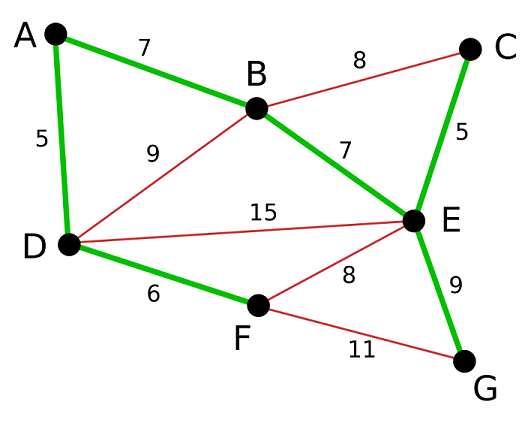
图是一种抽象数据类型（ADT），是一种由有限个结点（node或vertex）和边（edge）组成的非线性数据结构。一个图由顶点集（set of vertices）V和边集（set of edges）E组成，记为G=(V, E)。如下图就是由顶点集V={0, 1, 2, 3, 4}和边集E={01, 04, 14, 12, 13, 23, 34}组成。

注意：线性表可以是空表，树可以是空树，但是图不可以是空图，也就是说，图中不能一个顶点都没有，图的边集可以为空，但是图的顶点集一定不为空。

图这种数据结构蛮有用的，比如上面的图可以表示一幅人际关系网，每个结点可以表示一个人，也可以表示城市道路的交通网等等。

0x01 图的种类

0x00 有向图

有向图（Directed graph或digraph），是图中用来连接各顶点的边带有方向的图。又有定义，边集E是有向边（也成为弧）的有限集合时所构成的图，如图：

上图可表示为：

$G_1=(V_1, E_1) \\ V_1=\{1,2,3,4\} \\ E_1=\{<1,2>,<1,4>,<2,4>,<3,1>,<3,2>,<4,3>\}$

注：在国外教材中，有向图的边集一般用字母 $A$ 来表示， $A$ 为arrow的首字母

其中在边集中我们用<V, W>来表示一条弧（arrows, directed edges, directed arcs或直接写为arc），这是一个有序组（ordered pairs），其中V和W为顶点，V称为弧尾（箭头的出发点, 英文讲叫做the tail of the arrow），W称为弧头（箭头所指向的点，英文讲为the head），这条弧称为从顶点V到W的弧（a path leads from V to W），也称V邻接到W。

0x01 无向图

与有向图相反的是，无向图（undirected graph）即为边没有方向的图，在边集中，每一条边是用无序组（unordered pairs）(V, W)来表示的，故边(V, W)和边(W, V)是完全相同的。如图：

上图可表示为：

$G_2=(V_2, E_2) \\ V_2=\{1,2,3,4,5,6\} \\ E_2=\{<1,2>,<1,5>,<2,3>,<2,5>,<3,4>,<4,5>,<4,6>\}$

0x02 连通图

连通图（connected graph）：在无向图中，若从顶点v到顶点w有路径存在，则称v和w是连通的，若图中任意两个顶点都是连通的，则称此图为连通图。否则称为非连通图（disconnected graph）。如果一个图有N个结点，并且有小于N-1条边，则此图必为非连通图。一个仅有一个顶点的图是连通图。下图中，若把顶点0考虑在内，整个图不是连通图，除去0之外的部分为连通图：

无向图中的极大连通子图（maximal connected subgraph）称为连通分量（connected component）。相反还有极小连通子图（minimal connected subgraph），极小连通子图既要保持图连通又要是边数最小的子图。图的连通分量不一定是生成树，因为连通分量有可能包含回路。

极大连通子图为无向连通图的本身，极小连通子图为无向图的生成树。

一个具有N个结点的无向图，保证其在任何情况下都是连通的，需要的最小的边数为： $\frac{(N-1)(N-2)}{2}+1$ ，原因很简单要让N-1个结点构成无向完全图，然后再附加一条边，这样就可以保证在任何情况下都是连通的了。

含有e条边的非连通无向图，最少含有多少个顶点？

考虑最极端的情况，这个非连通无向图由一个完全图加一个孤立的结点构成，即这e条边全部都在那个完全图里即：

$\frac{N(N-1)}{2}=e$

解方程解出一个N来，然后N+1加上一个孤立的结点，即为最后结果

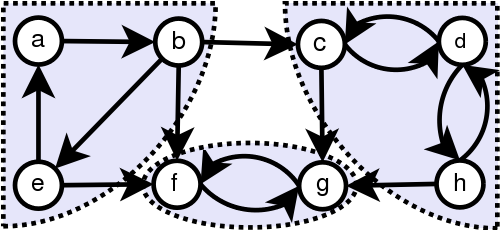
强连通图（strongly connected graph）：如果在有向图中，从任意顶点v和任意顶点w之间都存在从v到w的路径和从w到v的路径，那么称此图为强连通图。下图中阴影部分的子图为强连通图：

有向图中的极大强连通子图称为有向图的强连通分量。

TL;DR

由顶点集 $V_1=\{a,b,e\}$ 和顶点集 $V_2=\{f,g\}$ 共同构成的图不是强连通图，原因如下：从顶点b出发可以经过路径bfg抵达顶点g，但是从顶点g出发却没有一条路径可以抵达顶点b，所以顶点b和顶点g直接不是强连通的，所以由顶点集 $V=V_1\bigcup V_2$ 构成的图不为强连通图。

DFS和BFS算法可以用来计算图的连通分量数，因为一次遍历必然能将一个连通图中的所有顶点都访问到。

0x03 其他图

简单图（simple graph或strict graph）：一个图G中如果不存在重复边，不存在从顶点到自身的边，则为简单图。与之相对的则为多重图（Multigraph）。

无向完全图（complete graph）：如果图的任意两个节点之间都存在边，则称该图位无向完全图，如下：

含有 $N$ 个顶点的无向完全图有 $\frac{N(N-1)}{2}$ 条边。

有向完全图（complete digraph）：如果在有向图中，任意两个顶点都存在方向相反的两条弧，那么该图位有向完全图。

子图（subgraph）：设有2个图 $G_1=(V_1, E_1)$ 和 $G_2=(V_2, E_2)$ ，若 $V_2$ 是 $V_1$ 的子集且 $E_2$ 是 $E_1$ 的子集，那么称 $G_2$ 为 $G_1$ 的子图。若满足 $V_1=V_2$ 则称 $G_2$ 为 $G_1$ 的生成子图。注意并非 $V$ 和 $E$ 的任意子集都能构成 $G$ 的子图，因为有些子集的组合可能不是图。

边数很少的图称之为稀疏图（sparse graph），反之则为稠密图（dense graph）。

0x02 基本概念

0x00 度

图中一个顶点的度（degree或valency）即为以该顶点为一个端点的边的数目。

对于无向图而言，顶点v的度是指依附于该顶点的边的条数，记为TD(v)。

国外教材上一般把顶点的度记为 $\deg(v)$ ，并且将入度记为 $\deg^-(v)$ ，将出度记为 $\deg^+(v)$ ，此处指明的TD即为Total Degree的缩写。

无向图的全部顶点的度之和等于边数的两倍，即有如下等式成立：

$\sum_{i=1}^n\deg(v_i)=2\times e$

其中n为顶点的个数，e为边的条数。因为每条边都和两个顶点相互关联。

有向图中顶点的度又分为入度（indegree）和出度（outdegree），并且一张图总的度数等于其入度及出度之和。

有向图中入度之和等于出度之和等于边的条数，因为每个有向边都有一个起点和一个终点，即有如下等式成立：

$\sum_{i=1}^n\deg^-(v_i)=\sum_{i=1}^n\deg^+(v_i)=e$

在邻接矩阵表示法中，某个结点的度为这个结点所对应的行以及其所对应的列中的非零元素之和。

0x01 路径及回路

从顶点v到顶点w的路径是指从v到w的一个顶点序列，路径上边的数目称之为路径长度。一条路径中，第一个顶点与最后一个顶点相同的路径称之为回路或者环，如果一个图有N个顶点，并且有大于N-1条边，则此图中一定有环。

0x03 图的基本存储方式

0x00 邻接矩阵法

邻接矩阵法（Adjacency matrix）就是用一个一维数组存储图中的顶点信息，用一个二维数组（邻接矩阵）存储图中边的信息（各顶点的邻接关系）。

结点数为 $N$ 的图的邻接矩阵是 $N \times N$ 的，将这个矩阵记为 $A$ ，A[i][j]=1的条件是图中存在边 $(v_i,w_j)$ 或 $<v_i,w_j>$ 。否则A[i][j]=0。对于带权图而言，当边存在时，其邻接矩阵的取值为当前边的权值，不存在时一般取 $0$ 或 $\infty$ 。

使用邻接矩阵法存储图的空间复杂度为 $O(N^2)$ 。我们可以通过使用STL中的map将这个二维数组尽可能地压缩一下，当然最坏情况下还是要占用 $N^2$ 的空间的，例如将邻接矩阵定义为：

1
2
3

std::map<int, std::map<int, int>> arcs;
          ^             ^    ^
         顶点v        顶点w  权值或是否存在路径

这样如果我们试图判断边 $(v,w)$ 是否存在时，可以使用如下代码：

1	arcs.find(v) != arcs.end() && arcs[v].find(w) != arcs[v].end()

为什么使用上述语句而不直接使用如下的形式判断：
1
arcs[v][w] ? "Yes" : "No"
上面的这种形式对于map来说是很不安全的，原因很简单，当这个map里面并没有这一项的时候，你使用上面的这种形式判断是否存在此项，map也会给你创建出一个来，也就是说即便你没有对map进行插入操作，你使用[]运算符判断是否存在，map也会给你把这一项创建出来。

我们可以在STL的源代码里看到如下的代码：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
template<class _Keyty,
		class... _Mappedty>
		_Pairib _Try_emplace(_Keyty&& _Keyval,
			_Mappedty&&... _Mapval)
		{	// fail if _Keyval present, else emplace
		iterator _Where = _Mybase::lower_bound(_Keyval);
		if (_Where == _Mybase::end()
			|| _DEBUG_LT_PRED(_Mybase::_Getcomp(),
				_Keyval, _Mybase::_Key(_Where._Ptr)))
			return (_Pairib(
				_Mybase::emplace_hint(_Where,
					piecewise_construct,
					_STD forward_as_tuple(
						_STD forward<_Keyty>(_Keyval)),
					_STD forward_as_tuple(
						_STD forward<_Mappedty>(_Mapval)...)),
				true));
		else
			return (_Pairib(_Where, false));
		}
// 对其中的emplace_hint的代码如下：
	template<class... _Valty>
		iterator emplace_hint(const_iterator _Where, _Valty&&... _Val)
		{	// insert value_type(_Val...) at _Where
		_Nodeptr _Newnode = this->_Buynode(_STD forward<_Valty>(_Val)...);
		return (_Insert_hint(_Where, _Newnode->_Myval, _Newnode));
		}
当判断条件_Where == _Mybase::end()成立时，也就是当前map中并没有这一项时，他就会执行调用函数emplace_hint在_Mybase::end()处（使用默认构造函数）新建这一项。而且此时函数会返回新创建的这一项，多数情况下，我们仅仅是为了判断此项是否存在，而不希望其不存在时还要把这一项创建出来，所以判断key是否存在于map中，我们可以使用其find函数，检查其返回值是否等于map.end()。

使用邻接矩阵法存储图时，有如下特点：

无向图的邻接矩阵一定是对称矩阵，有偶数个边表结点，并且唯一。
无向图的邻接矩阵第i行的非零元素的个数恰好是图第i个结点的度。
有向图的邻接矩阵第i行的非零元素的个数恰好是图第i个结点的出度，第i列的非零元素的个数恰好是图第i个结点的入度。
邻接矩阵法适合存储稠密图。
使用邻接矩阵法可以快速确定任意两个结点之间是否有边相连，因为数组随机访问的效率要远远高于链表（对应为邻接表）。

假设一个图的邻接矩阵为A，则 $A^m$ 中第 $i$ 行和第 $j$ 列元素所代表的含义为：图中从顶点 $i$ 到顶点 $j$ 长度为m的路径条数。这个 $A^m$ 的计算方法就是你在线性代数里面学的那一套。

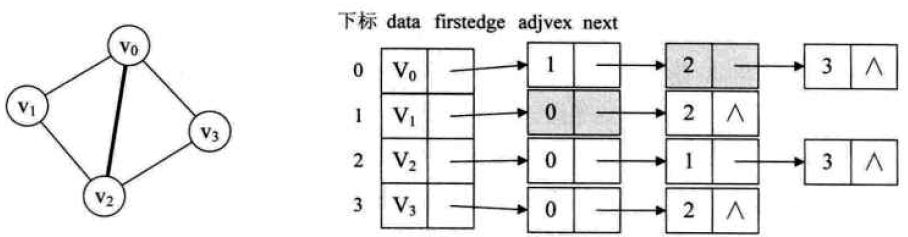
0x01 邻接表法

邻接表（Adjacency list）主要是为了解决使用临界矩阵存储稀疏图时空间大量浪费的问题。邻接表就是对图中的每一个顶点都建立一个单链表，来存储当前结点所有的边，对于有向图而言则存储所有的出边（就是从当前结点出发到对方结点的点）。

先给出一个用单链表实现的：

// 表结点（表示图的边）
struct Arcnode {
   int adjvex;                  // 这条边所指向顶点位置
   struct Arcnode *nextarc;     // 指针指向下一条边
};
// 表头结点（表示图的顶点）
struct VNode {
   int data;                    // 顶点数据，这里用字符表示
   struct Arcnode * firstarc;   // 指针指向第一条边 
};
// 图
struct MGraph {
   struct VNode vexs[100];
   int vexsnum, arcnum;          // 顶点数，边数
} *g;

如果是使用C++的话，还可以用这个实现：

1	std::vector<std::vector<int>> graph;

因为vector本身就是一个可动态扩容的数组，其初始情况下默认分配一段较小的存储空间，随着存储规模的增长，其会动态扩容。这种方法严格意义上来说其实不能算为邻接表。

使用邻接表存储有如下特点：

如果G为无向图的话，那么其所占用的存储空间为 $|V|+2|E|$ ，因为同样的一条边会在邻接表中出现两次。
如果G为有向图的话，那么其所占用的存储空间为 $|V|+|E|$ 。
邻接表适合存储稀疏图。因为这将极大地节省存储空间。
在邻接表中，给定一顶点，可很快地找到其临边，给定一条边，也可以很快判定这条边在图中是否存在，但是在邻接矩阵中，因为使用单链表去实现，所以相同的操作往往需要扫描一行，所以时间复杂度为 $O(N)$ 。
图的邻接表并不唯一，这往往取决于建立邻接表的算法以及输入序列。
有向图的邻接表存储中，顶点在边表中出现的次数即为顶点的入度。

0x02 十字链表

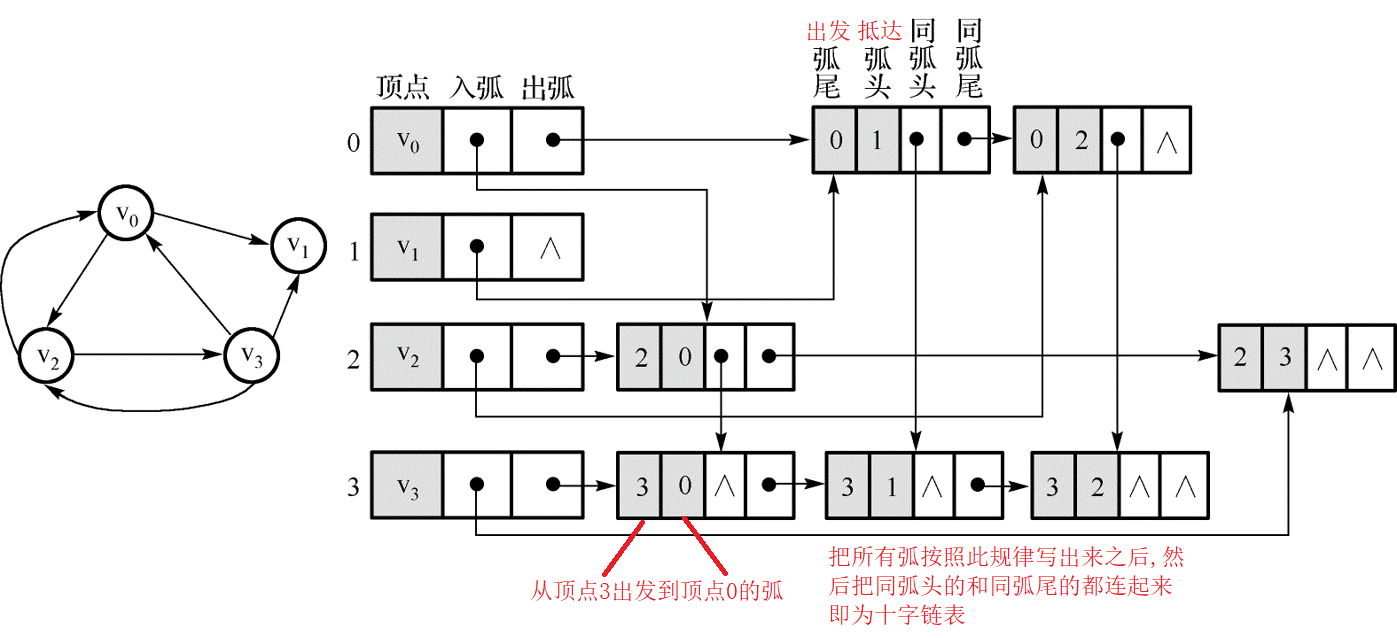
十字链表（Orthogonal list）是有向图的一种链式存储方式。语言不是很好描述，看图：

其中：

入弧表示箭头指向当前结点的弧长，出弧表示从当前结点出发到别的结点的弧。

弧头表示箭头所指向的顶点，弧尾表示发出箭头的顶点。

struct ArcNode      // 弧
{
    int head, tail; // 该弧的头尾顶点
    OLNode *right;  // 用来记录同弧尾的顶点
    OLNode *down;   // 用来记录同弧头的顶点
};

struct VNode           // 顶点表
{
    ArcNode *firstin;  // 入弧
    ArcNode *firstout; // 出弧
    int value;         // 顶点信息
};

顶点之间可使用顺序存储。

图的十字链表不唯一，但是一个十字链表可准确地确定一个图。

0x03 邻接多重表

邻接多重表（Adjacency Multi List）是无向图的另一种链式存储结构。

在邻接表中，容易求得顶点和边的信息，但是如果需要判断两个顶点之间是否存在边，或者进行边的删除操作，那么需要在两个链表之间进行遍历，效率较低。

如图，一个用邻接表表示的图中，如果想要删除 $<v_0,v_2>$ 这条边，则需要对邻接表中的两个结点进行删除。

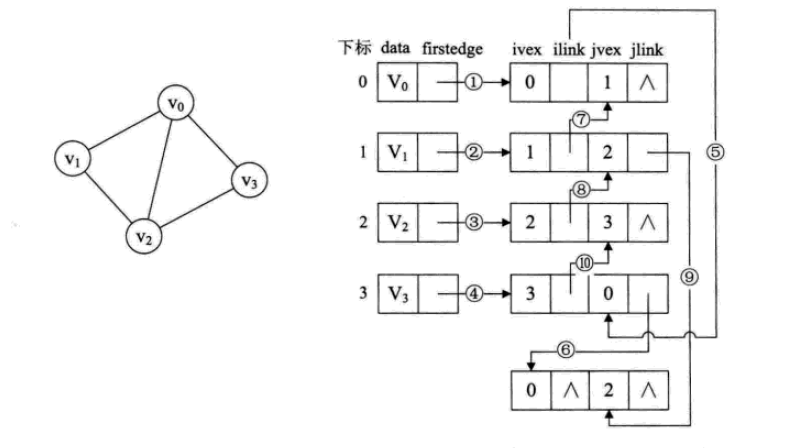
在邻接多重表中每一条边用一个结点表示，先看图：

在一个邻接多重表中，ivex和jvex代表了当前边所连接的两个顶点，ilink指向下一条依附于ivex的边，jlink指向下一条依附于jvex的边。

在有些实现中，存储边信息的结点往往还多2个域，即mark标识域，即标记当前边有没有被搜索过，以及info域，指向和边相关的各种信息。

0x04 图的遍历

0x00 广度优先搜索

广度优先搜索（Breadth-first search, BFS）的基本思路就是，先访问起始顶点v，然后再依次访问顶点v的各个邻接顶点，然后再依次访问这些邻接顶点的所有邻接节点，依次类推，直到图中所有的顶点均被访问过为止。这个过程有点像我们二叉树的层序遍历。如图：

先来做一道紧张而又刺激的ACM题目来体验一下无向图的BFS的流程吧：

数据结构实验之图论一：基于邻接矩阵的广度优先搜索遍历

AC代码如下：

#include <iostream>
#include <map>
#include <set>
#include <queue>

int main()
{
    int n;
    std::cin >> n;
    int k, m, t;
    int arc1, arc2;
    while (n--)
    {
        std::map<int, std::set<int>> graph;
        std::cin >> k >> m >> t;
        // 使用邻接矩阵来存储图
        for (int i = 0; i < m; ++i)
        {
            std::cin >> arc1 >> arc2;
            graph[arc1].emplace(arc2);
            graph[arc2].emplace(arc1);
        }
        std::set<int> visited;
        std::queue<int> queue;
        visited.emplace(t);
        queue.push(t);
        while (!queue.empty())
        {
            std::cout << queue.front() << " ";
            std::set<int> &adj = graph[queue.front()];
            queue.pop();
            for (auto iter = adj.begin(); iter != adj.end(); ++iter)
            {
                if (visited.find(*iter) == visited.end())
                {
                    visited.emplace(*iter);
                    queue.push(*iter);
                }
            }
        }
        std::cout << std::endl;
    }
    return 0;
}

无论是使用邻接矩阵还是邻接表来实现，广度优先搜索总要借助一个辅助队列，所以，在其最坏状况下的空间复杂度为 $O(|V|)$ ，此时图中的每一个顶点都要入队一次。在使用邻接表的情况下，每个顶点都要搜索一次，故时间复杂度为 $O(|V|)$ ，在搜索任一顶点的邻接点时，每条边至少访问一次，故时间复杂度为 $O(|E|)$ ，所以对于邻接表来说，算法的总时间复杂度为 $O(|V|+|E|)$ 。当采用邻接矩阵存储时，查找每个邻接点所需的时间为 $O(|V|)$ ，所以算法的总时间复杂度为 $O(|V|^2)$

0x01 深度优先搜索

深度优先搜索（Depth-first search或DFS）类似于二叉树的先序遍历，就是搜索的时候先尽可能深地搜索一个图，其基本的流程是先访问某一起始顶点，然后从此结点出发访问与其邻接的任意顶点，然后尽可能深地向下访问，当不能继续向下访问时，依次退回到最近被访问的顶点，若还有顶点没有访问到则从该点开始继续上面的搜索过程，直到所有顶点都被访问过为止。

先来一道ACM题目体验一下这个过程：

数据结构实验之图论二：图的深度遍历

代码如下：

#include <iostream>
#include <vector>

void DFS(std::vector<std::vector<bool>>& graph, bool *visited, int from, std::vector<int>& result)
{
    visited[from] = true;   // 标记当前结点已被访问
    result.push_back(from);
    for (int i = 0; i < graph.size(); ++i)
    {
        // 如果i这个顶点没有被访问过, 且与from顶点之间存在边的话
        if (!visited[i] && graph[from][i])
        {
            // 向下递归遍历
            DFS(graph, visited, i, result);
        }
    }
}

std::vector<int> DFS(std::vector<std::vector<bool>>& graph)
{
    bool *visited = new bool[graph.size()]{};
    std::vector<int> result;
    for (int i = 0; i < graph.size(); ++i)
    {
        if (!visited[i])
        {
            DFS(graph, visited, i, result);
        }
    }
    delete[] visited;
    return result;
}

int main()
{
    int n;
    std::cin >> n;
    int k, m;
    int u, v;
    while (n--)
    {
        std::cin >> k >> m;
        std::vector<std::vector<bool>> graph(k, std::vector<bool>(k, false));
        for (int i = 0; i < m; ++i)
        {
            std::cin >> u >> v;
            // 无向图的邻接矩阵一定不要忘了uv和vu两个都要置为true
            graph[u][v] = true;
            graph[v][u] = true;
        }
        // 输出DFS遍历序列
        std::vector<int> result = DFS(graph);
        for (int i = 0; i < result.size() - 1; ++i)
        {
            std::cout << result[i] << " ";
        }
        std::cout << result[result.size() - 1] << std::endl;
    }
    return 0;
}

图的邻接矩阵表示是唯一的，但对于邻接表来说，如果边的输入次序不同，生成的邻接表也不同，因此对于同样一个图，基于邻接矩阵得到的DFS和BFS序列是唯一的，但是基于邻接表是不唯一的。

让我们来琢磨一个办法，把DFS中的递归消除掉吧！还是上面的那个题，下面的这段非递归的代码琢磨了我老长时间：

std::vector<int> DFS(std::vector<std::vector<bool>>& graph)
{
    std::vector<bool> visited(graph.size(), false);
    std::vector<int> result;
    std::stack<int> stk;
    stk.push(0);
    visited[0] = true;
    result.push_back(0);
    while (!stk.empty())
    {
        int top = stk.top();
        int i;
        for (i = 0; i < graph.size(); ++i)
        {
            if (!visited[i] && graph[top][i])
            {
                stk.push(i);
                result.push_back(i);
                visited[i] = true;
                break; // 注意此处要break掉
                // 看如下情况
                //      0
                //     / \ 
                //    2   4
                //   / \
                //  1   3
                // 当走到2时因为2还有1和3两个邻接的顶点没有被访问过
                // 深度优先，所以我们要先遍历1和3然后再访问4
                // 所以在1和3访问之前我们不能把4入栈
                // 要不然入栈之后先出来的就是4了
            }
        }
        // 如果当前顶点还有邻接的顶点没有被访问过的话
        // 那就沿着当前结点继续访问下去
        // 如果当前顶点的全部邻接顶点都被访问过了
        // 也就是当i == graph.size()时
        // 那就将当前结点退栈
        if (i == graph.size())
        {
            stk.pop();
        }
    }
    return result;
}

为了保持简介，此处仅给出进行DFS遍历的那个函数，DFS是一个递归算法，转换成非递归也需要额外占用一个工作栈，所以其空间复杂度为 $O(|V|)$ ，当使用邻接矩阵时，查找每个顶点邻接点所需要的时间为 $O(|V|)$ ，故其总的时间复杂度为 $O(|V|^2)$ ，当使用邻接表时，查找每个顶点邻接点的时间为 $O(|E|)$ ，所以使用邻接表总的时间复杂度为 $O(|V|+|E|)$ 。

0x02 判断图中是否有环

这是一个通用的方法，既适用于有向图又适用于无向图，算法思路：

统计这个图中每个结点的入度数
有向图找入度为0的点，无向图找度为1的点
删除这些点及其所有的边并消减这些被删去的边所对应的结点的入度值
重复2直到所有点入度为0则为无环图，如果找不到入度为0的点则为有环图

使用此算法来解一道紧张而又刺激的LeetCode题目：207. Course Schedule

class Solution {
public:
    bool canFinish(int numCourses, std::vector<std::pair<int, int>>& prerequisites) {
        std::vector<std::vector<int>> graph(numCourses, std::vector<int>(numCourses));
        std::vector<int> degree(numCourses, 0);
        std::vector<int> visited(numCourses, 0);
        for (std::pair<int, int> pair : prerequisites)
        {
            graph[pair.first][pair.second] = 1;
            ++degree[pair.second];
        }
        // 进行n次循环
        for (int k = 0; k < numCourses; ++k)
        {
            // 遍历所有的点，找入度为0的点
            for (int i = 0; i < numCourses; ++i)
            {
                // 如果没有被访问过且入度为0
                if (!visited[i] && degree[i] == 0)
                {
                    visited[i] = 1;
                    // 消减此结点能够到达的结点的入度值
                    for (int j = 0; j < numCourses; ++j)
                    {
                        if (graph[i][j] != 0)
                        {
                            --degree[j];
                        }
                    }
                }
            }
        }
        // 此过程完结之后如果仍然存在入度不为0的点，则有环
        for (int i = 0; i < numCourses; ++i)
        {
            if (degree[i] != 0)
            {
                return false;
            }
        }
        return true;
    }
};

运行时间68ms超越了9.7%的人，够慢，我喜欢，这个算法唯一的好处就在于它够简单，通俗易懂容易理解。使用邻接矩阵做图的存储时，时间复杂度为 $O(|V|^3)$ 。

同样更快速的话，还可以使用DFS深度优先搜索的算法来进行检测，基本思路为：

DFS不断递归往深处走
一旦发现DFS的下一个结点时已经访问过了的结点则图中存在环

注意：使用这种思路，对于有向图要设置三种状态，0未访问，1访问过了，-1正在从此结点开始往下DFS，对于无向图只需要设置前2种状态即可了，原因很简单，如下：

      0                             0
    ╱   ╲                         ╱   ╲
   └     ┘                       ╱     ╲
  1------->2                    1-------2
这个有向图不存在环             这个无向图存在环

TL;DR

如果对有向图也仅设0未访问，1访问过了这2种状态的话，对于上图左边的那个有向图而言，访问从0开始->1->2，这时0,1,2三个结点都被标记为了已访问，此时递归回溯到结点0，又从0开始访问2，这时2已经是已访问状态了，此时就会被错误地判定成有向图中存在环，而实际情况是有向图中不存在环。

还是上面那个题使用寻找访问过的结点的思路的非递归版DFS算法如下：

class Solution {

    // 有环返回true, 无环为false
    bool dfs(std::vector<std::vector<int>>& graph)
    {
        std::stack<int> stk;
        // 0未访问，1访问过了，-1正在从此结点开始往下DFS
        std::vector<int> visited(graph.size(), 0);
        // 不能单纯地从0结点开始判断
        // 因为如果有向图中0结点的出度为0
        // 那么一趟之后剩下的结点都没有判断函数就返回了
        // 所以需要对每一个没有访问到的结点都执行一遍DFS
        for (int j = 0; j < graph.size(); ++j)
        {
            if (visited[j] == 0)
            {
                stk.push(j);
                while (!stk.empty())
                {
                    int top = stk.top();
                    visited[top] = -1;
                    int i = 0;
                    for (; i < graph.size(); ++i)
                    {
                        if (visited[i] == 0 && graph[top][i])
                        {
                            stk.push(i);
                            break;
                        }
                        else if (visited[i] == -1 && graph[top][i])
                        {
                            return true;
                        }
                    }
                    if (i == graph.size())
                    {
                        stk.pop();
                        visited[top] = 1;
                    }
                }
            }
        }
        return false;
    }

public:
    bool canFinish(int numCourses, std::vector<std::pair<int, int>>& prerequisites) {
        std::vector<std::vector<int>> graph(numCourses, std::vector<int>(numCourses));
        std::vector<int> visited(numCourses, 0);
        for (std::pair<int, int> pair : prerequisites)
        {
            graph[pair.first][pair.second] = 1;
        }
        return !dfs(graph);
    }
};

使用DFS算法还有一个思路就是连通分量数，众所周知DFS算法可以用来求解图的连通分量数，假设求解出来的连通分量数为P则，如果图的总边数E>结点数V-连通分量数P，那么图中就一定有环，注意此方法仅适用于无向图，如下是一个用于求解连通分量数的DFS算法：

// 返回连通分量数P
int dfs(std::vector<std::vector<int>>& graph)
{
    std::stack<int> stk;
    int p = 0;
    // 0未访问，1访问过了
    std::vector<int> visited(graph.size(), 0);
    for (int j = 0; j < graph.size(); ++j)
    {
        if (visited[j] == 0)
        {
            ++p; // 连通分量个数+1
            // 下面是一趟标准的无递归DFS流程
            stk.push(j);
            visited[j] = 1;
            while (!stk.empty())
            {
                int top = stk.top();
                int i = 0;
                for (; i < graph.size(); ++i)
                {
                    if (visited[i] == 0 && graph[top][i])
                    {
                        stk.push(i);
                        visited[i] = 1;
                        break;
                    }
                }
                if (i == graph.size())
                {
                    stk.pop();
                }
            }
        }
    }
    return p;
}

0x05 最小生成树

一个连通图的生成树（Spanning Tree）是图的极小连通子图，它包含图中所有顶点，并且含尽可能少的边。这就意味着，对于生成树而言，若砍去它的一条边，就会使生成树变成非连通图。若增加一条边，就会形成一条回路。

对于带权连通无向图而言，生成树不同，每棵树的权值也可能不同，其最小生成树（Minimum Spanning Tree）就是图的所有生成树中，权值之和最小的那一个。当图中所边的权值均互不相等时，其最小生成树唯一。如图的边数比顶点数少1，也就是图本身就是一棵树时，则图本身就是图的最小生成树。

最小生成树有如下性质：

最小生成树的边数等于顶点数减一
最小生成树的边的权值之和总是唯一的，但是最小生成树是不唯一的。

0x00 Prim’s Algorithm

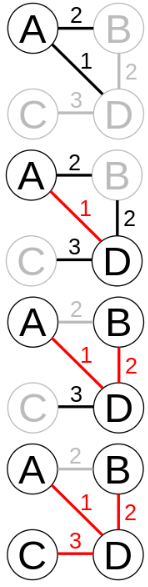
Prim’s 算法描述起来其实挺简单的，看图：

类似于贪心的策略，走一步就选一步的最优解，上图中的红线就是Prim’s所形成的结果，首先从顶点A开始，可以到达B和D，到达B的代价为2，而到达D的代价为1，所以选择代价最小的进行连接，然后从D开始可以到达B和C，然后继续选择代价最小的B，此时我们在B上，A已经在树上了，所以我们退回到D，继而到达最后一个顶点C，算法完成。

Prim’s 算法的时间复杂度为 $O(|V|^2)$ ，其不依赖于|E|，所以适用于求解边稠密的图的最小生成树。

0x01 Kruskal Algorithm

Kruskal算法是一种按权值递增的顺序来选择合适的边构造最小生成树的方法，算法的相关流程如下：

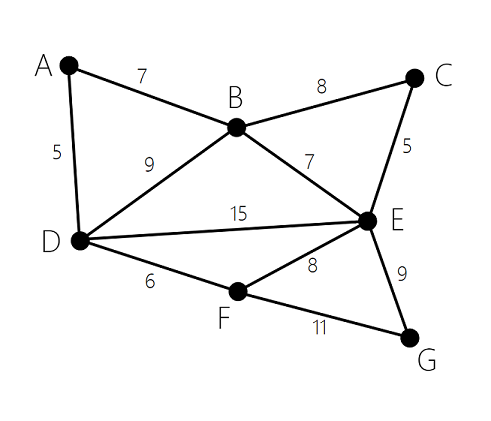
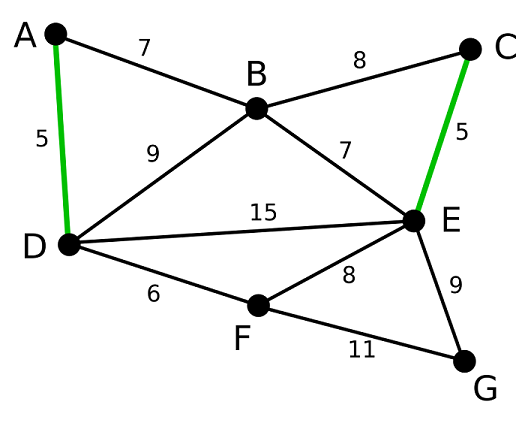
首先这是一个带权图：

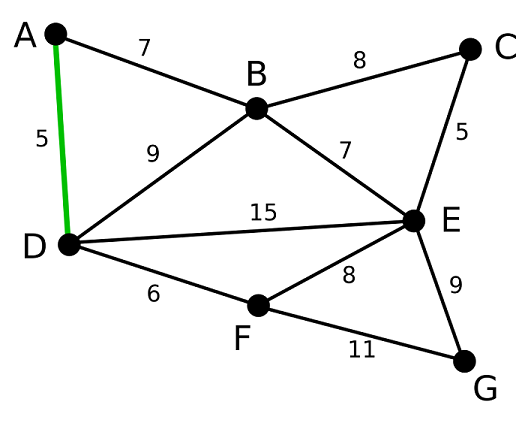
我们依次查找图的边，找到AD和CE是两个权值最小的边，两者权值均等于5，我们中两者中随机选择一条加入最小生成树，假设说选择AD边，用绿色将其标注出来。

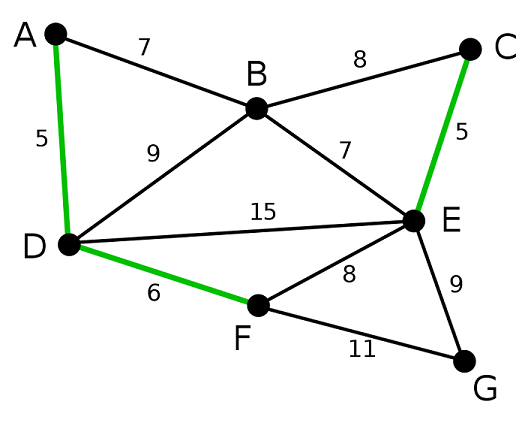
再剩下的边中再继续查找权值最小的边，此时CE为权值最小的边，将其加入树中：

依重复执行上述流程，将DF加入图中：

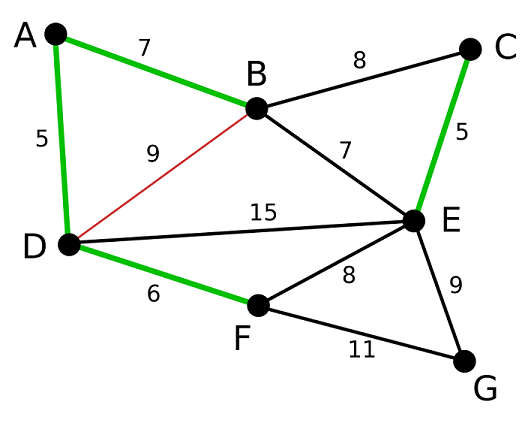
此时图中还没有加入树的权值最小的边为AB和BE，随机选择，此处选择将AB加入树中，加入树中之后，BD之间已经有了通路BAD了，所以再次查找权值最小的边时，无需查找BD，将BD用红颜色标注出来，代表无需查找：

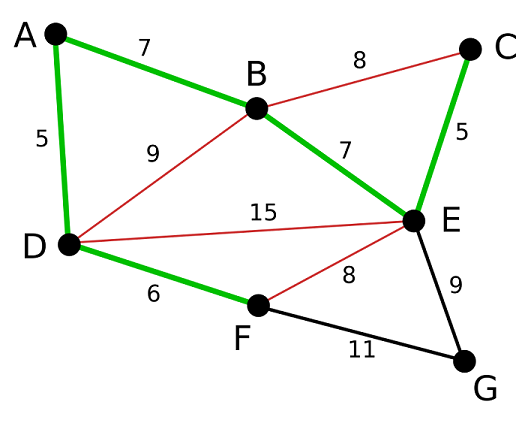
在剩下的边中，权值最小的为BE，将BE加入树中，此时BC之间有通路BEC，DE和BF之间分别有通路DABE和BEF，所以将多余的边BC, DE, EF用红笔标注出来，以后不再访问：

此时仅有边EG和FG了，选出其权值最小的边EG将其连接起来，至此图中所有顶点均被连接，算法完成，图中绿色部分即为最小生成树：

通常在Kruskal算法中使用堆来存放边的集合，这样每次选择最小权值的边只需要 $O(\log|E|)$ 的时间，Kruskal算法整体的时间复杂度为 $O(E\log|E|)$ ，Kruskal算法适用于边稀疏而顶点较多的图。

0x06 最短路径

对于一个带权图来说，从一个顶点到另一个顶点的一条路径上所经过的边的权值之和称为该路径的带权路径长度（Weighted Path Length简称WPL），带权路径长度最短的那条路径即为最短路径（Shortest path）。

最短路径问题可分为两类，第一种为单源最短路径（Single-source shortest paths），即为从图中某一顶点出发到其他各顶点的最短路径，可使用Dijkstra算法求解。第二种为求每一对顶点间的最短路径（All-pairs shortest paths），可使用Floyd算法求解。

0x00 Dijkstra’s Algorithm

Dijkstra算法适用于求从某个顶点出发到其余顶点的最短路径，算法流程如下：

如上图，从顶点1开始寻找一条到顶点5的最短路径，首先使用一个数组记录从顶点1开始到其余任意顶点的最短路径长度，将这个数组记为dist，其初始值为 $\infty$ ，然后从节点1开始访问其邻接点，并将其邻接点的路径长度存入数组dist中，然后再依次抵达这些邻接点，再从这些邻接点开始继续访问下面的结点，每次访问将路径长度加起来，然后比较新的路径的路径长度与dist存放的路径长度的大小，将小的那个放入dist数组中，依次向下，直到走完了所有能抵达的目标顶点的路径，此时，dist数组中存放的值即为最短路径。

使用此算法时，人们可能只希望找到从某一个顶点到另一个特定顶点的最短路径。但是这和求解从源顶点到剩余所有顶点的最短路径一样复杂，其时间复杂度为 $O(|V|^2)$ ，如果希望求解所有结对顶点直接的最短路径，则使用此算法的时间复杂度为 $O(|V|^3)$ 。

注意如果图中有边的权值为负，Dijkstra算法不再适用，其主要适合求解带回路的带权图的最短路径。

0x01 Floyd’s Algorithm

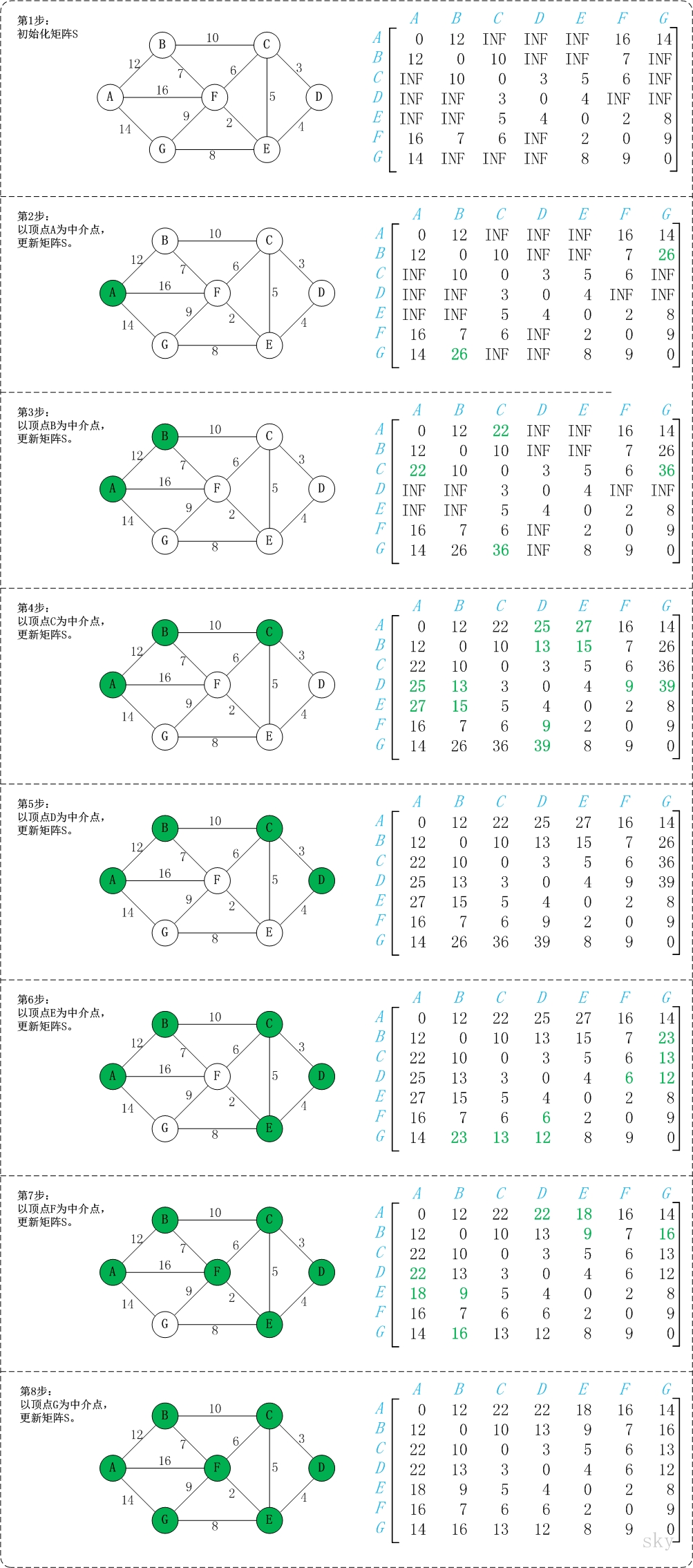
Floyd算法的全称应该叫Floyd–Warshall Algorithm，主要用于求解各顶点之间的最短路径，即求解任意两个顶点之间的最短路径以及最短路径长度。

看图就都明白了：

Floyd算法的时间复杂度为 $O(|V|^3)$ ，同时此算法允许图中有权值为负的顶点，但是不允许有带负权值的边组成的回路。

0x07 拓扑排序

先来介绍几个概念：

有向无环图：即一个没有环的有向图，英文讲为Directed acyclic graph简写为DAG图
AOV网：如果一个DAG图表示一个工程，其顶点表示活动，有向边 $<V_i，V_j>$ 表示活动 $V_i$ 必需先于 $V_j$ 进行，则称这种有向图为顶点表示活动的网络，记为AOV（Activity on Vertex）网

对于一个有向无环图的顶点组成的序列，当满足如下条件时，称为该图的一个拓扑排序（Topological sort）：

每个顶点都仅出现一次
若顶点A在序列中排在B的前面，那么图中不存在从B到A的路径，因为活动A要先于活动B之前发生

给定一个DAG图，获取拓扑排序序列方法：

从DAG图中选出一个没有前驱（入度为0）的顶点并输出
从图中删除该顶点以及所以以它为起点的有向边
重复上述过程直到DAG图为空，或当前图中不存在无前驱的顶点为止（此时图中必存在环）。

拓扑排序的时间复杂度为 $O(|V|+|E|)$ ，其中 $+|E|$ 的原因是输出每个结点的同时还需要删除以它为起点的边。

由于DAG图中各顶点的地位相等，如果按照其拓扑排序的结果重新安排顶点的序号，生成的新的DAG图用邻接矩阵表示将会是一个三角矩阵。对于一个普通的图，如果其邻接矩阵是三角矩阵，则存在拓扑排序序列，反之不一定成立。

同时，可以使用DFS算法得到一个图的拓扑排序序列，对于一个有向无环图而言，进行DFS算法，退出DFS栈的序列即为一个逆拓扑排序（反过来的拓扑排序序列）。

0x08 关键路径

在带权有向图中，以顶点表示事件，有向边表示活动，边上的权值表示完成该活动的开销，则称这种有向图为用边表示活动的网络为AOE（Activity On Edge）网。AOE网具有如下两个特征：

只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始
只有在进入某一顶点的各有向边所代表的活动都已经结束时，该顶点所代表的事件才能发生

AOE网中有且仅有一个入度为0的点（开始顶点，源点）和一个出度为0的点（结束顶点，汇点）。

在AOE网中，有些活动是可以并行进行的，从源点到汇点的有向路径可能由多条，并且这些路径长度可能不同。完成不同路径上的活动所需时间虽然不同，但是只要所有路径上的活动都完成了，整个工程才算是结束。因此，从源点到汇点的所有路径中，具有最大路径长度的路径称为关键路径。把关键路径上的活动称为关键活动。完成整个工程最短的时间即为关键路径的长度。